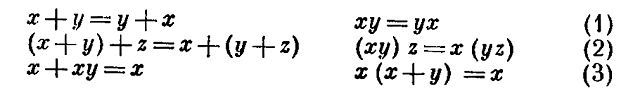
Приглашаем посетить сайт
СТРУКТУРА (В МАТЕМАТИКЕ)
В алгебре наз. С. (или решеткой) множество М, рассматриваемое вместе с двумя двухместными операциями (первой, условно называемой часто сложением и обозначаемой знаком +, второй, условно называемой умножением и обозначаемой соответственно знаком + или отсутствием знака), если выполняются три пары тождеств:
С. часто наз. также упорядоченное множество (см. Порядка отношение), в к-ром для любых двух элементов а и b: (I) есть такой элемент sup (а, b), к-рый обладает свойствами: a ≤ sup (a, b), b ≤ sup (a, b), если a ≤ x и b ≤ x, то sup (a, b) ≤ x; и (II) есть такой элемент inf (a, b), к-рый обладает свойствами: inf (а, b) ≤ a, inf (a, b) ≤ b, если x ≤ a и x ≤ b, то x ≤ inf (a, b) [элемент sup (a, b) наз. точной верхней границей, или верхней гранью, элементов а и b, элемент inf (а, b) - их точной нижней границей, или нижней гранью].
Если множество M вместе с двумя операциями является С. в первом смысле, то, определив на M отношение x ≤ у ≡ df x + у = у (где ≡ df - знак тождественности по определению), мы получим упорядоченное множество, являющееся С. во втором смысле [а именно, sup (a, b) = a + b; inf (a, b) = ab]. И обратно: если в упорядоченном множестве, являющемся С. во втором смысле, определить операции х + у ≡ df sup (x, у), x · y ≡ df inf (x, y), мы получим С. в первом смысле.
С. наз. дистрибутивной, если в ней выполняется тождество x (y + z) = xy + xz (4)
Дистрибутивная С. наз. б у л е в о й, если в ней, во-первых, есть два спец. элемента (первый из них можно условно назвать нулем и обозначить знаком 0, второй - единицей и обозначить, соответственно, знаком 1 ) такие, что х + 0 = х, х · 1 = х (5)
и, во-вторых, для любого элемента x есть такой элемент х', что x + х' = 1, х + х' = 0 (6)
(элемент х' наз. дополнением элемента х).
Булевы С. наз. также булевыми а л г е б р а м и (или алгебрами Буля, см. Алгебра логики). Важнейшим примером булевой С. является система всех подмножеств произвольного множества А, рассматриваемая вместе с операциями теоретико-множественного объединения и пересечения. Единицей этой С. является само множество А, нулем - пустое множество ø, дополнением произвольного подмножества X множества А является их разность: А X. В трактате Н. Бурбаки "Начала математики" (пер. с франц., М., 1965) слово С. является частью термина "структура данного рода" и родств. терминов. В свою очередь, термин "структура данного рода" определяется контекстуально. Если элемент нек-рого множества M, построенного из каких-то исходных множеств при помощи двух операций (прямого произведения и перехода к множеству всех подмножеств), обладает определ. свойствами, то говорят, что этот элемент задает на исходных множествах С. данного рода. Примерами С., или точнее родов структур, являются алгебраич. С. (группы, кольца и т.д.), топологич. С., структуры упорядоченного множества и т.п.
Лит.: Курош А. Г., Лекции по общей алгебре, М., 1962; Бурбаки Н., Теория множеств, пер. с франц., М., 1965 (Начала математики, ч. 1, кн. 1).
Ю. Шиханович. Москва.